2022.04.27
Решение задачи про приехавших раньше и опаздывающих.
Задача: Велосипедист должен попасть в место назначения к определенному сроку. Известно, что если он поедет со скоростью 15 км/ч, то приедет на 1 час раньше, а если со скоростью 10 км/ч, то опоздает на 1 час. С какой скоростью он должен ехать?
Ответ: 12 км/ч
Решение 1. Весы, принцип уравнивания.
- Пусть у нас два велосипедиста:
a) один быстрый, едет со скоростью 15 км/ч и проезжает все расстояние за t часов,
b) второй медленный, едет со скоростью 10 км/ч и проезжает расстояние за t+2 часа. Разница во времени медленного и быстрого равна 2-м часам, так как быстрый приезжает на час раньше, а медленный на час позже запланированного времени. -
Оба проезжают одинаковое расстояние, что позволяет их уравнять (получаем уравнение).
Остается рассмотреть оставшиеся части пути у быстрого и у медленного.
Чтобы решить уравнение его надо максимально упростить. Для этого можем убрать из рассмотрения одинаковые части в пройденных расстояниях.
Что одинаковое у медленного и быстрого? - Расстояние, которое проехал быстрый со скоростью медленного 10 км/ч*t и расстояние, которое проехал медленный за время быстрого 10 км/ч*t
-
Если быстрый поедет со скоростью медленного, то за каждый час его пройденный путь будет на 5 км меньше (не 15км, а 10км, не 30 км, а 20 км и т.д.), сколько часов движется, столько раз будет на 5 км меньше.
В итоге через время t ему останется еще проехать 5 км/ч * t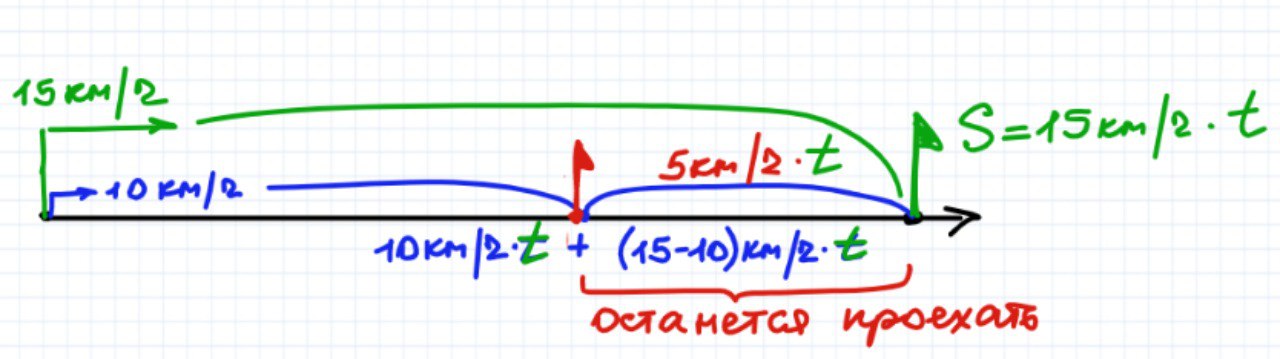
-
Если медленный едет столько времени, сколько быстрый, то через время t (время быстрого) ему останется ехать по времени еще 2 часа (разница времени быстрого и медленного) расстояние 2 ч*10 км/ч =20км

-
Таким образом, теперь у нас уравнены оставшиеся части пути быстрого и медленного 5 км/ч * t = 20 км/ч.
Что позволяет решить уравнение т.е. t = 4 часа -
Время быстрого позволяет найти время медленно +2часа и полный путь:
Весь путь 15 км/ч * 4 ч = 60 км или
10км/ч*6 ч = 60 км -
Время вовремя - время, за которое нужно проехать полный путь.
4 ч + 1 ч= 5 ч (поскольку быстрый приехал на 1 час раньше) -
Чтобы преодолеть путь 60 км вовремя (за 5 часов) скорость, с которой должен ехать велосипедист равна:
60 км : 5 ч = 12 км/ч
Ответ: 12 км/ч
Решение 2. Метод уравнений.
Пусть t часов - это время, необходимое велосипедисту, чтобы вовремя попасть в место назначения.
Тогда:
- двигаясь со скоростью 15 км/ч, он потратит (t – 1) часов, а
- двигаясь со скоростью 10 км/ч, он потратит (t + 1) часов.
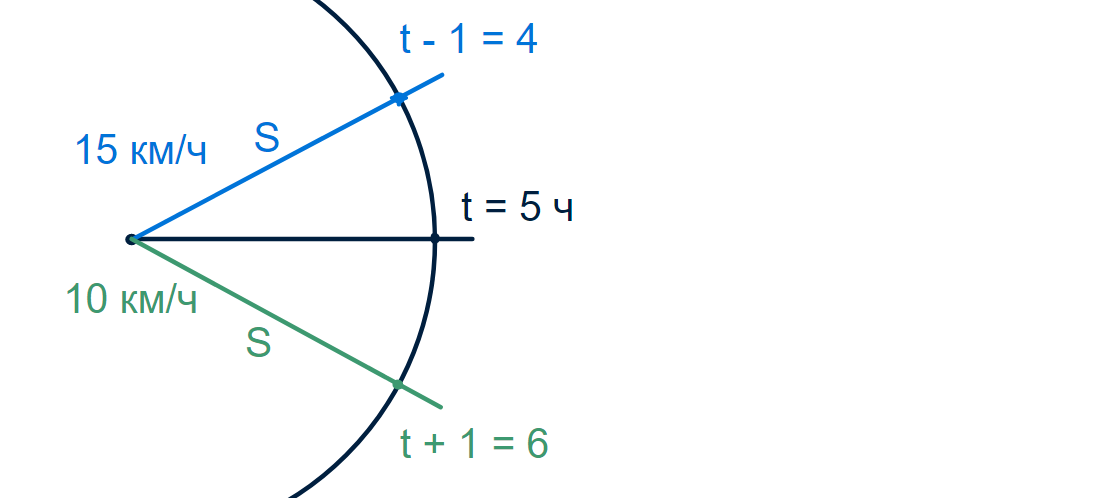
Так как в обоих случаях он проедет одно и то же расстояние, то можно составить уравнение:
15 * (t – 1) = 10 * (t + 1)
Решаем это уравнение:
15 t – 15 = 10 t + 10
5 t = 25
t = 5 ч
Найдем расстояние до места назначения:
10 * (t+ 1) = 10 *(5 + 1) = 60 км.
Найдем скорость, необходимую, чтобы приехать вовремя: 60 км : 5 ч = 12 км/ч.
Ответ: 12 км/ч
Решение задач на скорость. Типичные ошибки
5:2=2.5 + 10=12.5 [ км/ч ] - скорость, с которой он должен двигаться
Источники и прецеденты использования
Лицей Капицы
